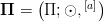
przy czym
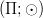jes grupą abelową, a potęgownie spełnia aksjomaty mnożenia przez skalar; dodatkowo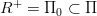 
2. W przestrzeni wprowadzamy pojęcie wymiarowej zależności. Pozwala to na wprowadzenie układu jednostek
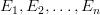(z definicji wymiarowo niezależnego). Każdą wielkość 
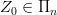można przedstawić w postaci: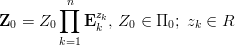
3. Twierdzenie o niezalezności
Jeżeli wielkości wymiarowe
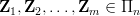wyrazimy w układzie jednostek wzorami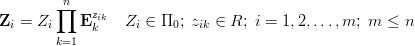
to żeby wielkości Z były wymiarowo niezależne potrzeba i wystarcza, żeby macierz utworzona z wykładników występujących w powyższym wzorze była rzędu m
4. W przestrzeni możemy mieć więcej niż jeden uklad jednostek.
5. Relacja rownoważnosci: dwie wielkości
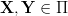mają ten sam wymiar gdy 
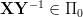. Relacja ta dzieli elementy przestrzeni wymiarowej na rozłączne klasy w ten sposób, że do jednej klasy należą elementy o tym samym wymiarze. W obrębie klasy można wprowadzićoperacje dodawania i odejmowania, liczyć granice ciągów i różniczkować.6. Zasadnicze znaczenie dla analizy wymiarowej ma pojęcie funkcji wymiarowej czyli funkcji o wartościach i argumentach wymiarowych:
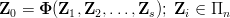
7. Jeżeli funkcja Φ spełnia warunki jednorodności wymiarowej (dla każdego zestawu
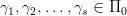istnieje takie 
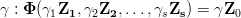) oraz niezmienniczości (dla przekształcenia Θ spełniona jest równość 
) nazywana jest funkcją wymiarowo jednorodną i niezmienniczą. Prawdziwe jest Twierdzienie π:8. Jeżeli w wymiarowo jednorodnej i niezmienniczej funkcji Φ argumenty
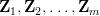sąwymiarowo niezależne, a argumenty 
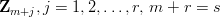są wymiarowo zależne, tzn. 
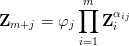to funkcja Φ ma postać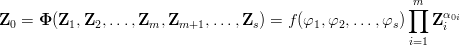
9. Twierdzenie π jest ważne, gdyż pozwala przekształcić funkcję wymiarową Φ do iloczynu funkcji liczbowej i pewnego wyrażenia wymiarowego. Pozwala to przenieść zadanie identyfikacji z przestrzeni wymiarowej do liczbowej.