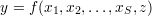
Niech nasz obiekt badań będzie opisany zależnością:
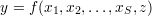 | (1) |
Mamy S wejść, jedno wyjście oraz dodatkową zmienną mającą wpływ na zachowanie obiektu, a mającą charakter „zaburzeń”.
Jeżeli przyjmiemy, że zaburzenia z mają charakter losowy nasza zależność z prostej zależności funkcyjnej przekształci się w zależność stochastyczną. Istotą tej zależności jest zależność rozkładu prawdopodobieństwa zmiennej losowej Y od wartości x przybranej przez zmienną losową X.1
Będziemy mówić, że zmienna losowa Y jest zależna stochastycznie od zmiennej losowej X, jeśli dystrybuanta F zmiennej losowej przy warunku X = x jest nie tylko funkcją wartości y zmiennej losowej Y , lecz także wartości x
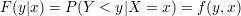 | (2) |
Budując opis matematyczny obiektu najbardziej interesuje nas wartość oczekiwana zmiennej losowej Y przy warunku X = x. Jeśli zachodzi:
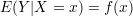 | (3) |
to mówimy o korelacji między zmiennymi losowymi Y i X.
Dokonujemy N pomiarów wartości x1,x2,…,xS oraz odpowiadających im wartości y. Dane te możemy zgrupować w tablicy wejść i wyjść
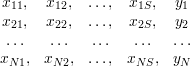 | (4) |
Naszym celem jest wyznaczenie charakterystyki zastępczej o postaci
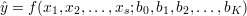 | (5) |
zawierającej K + 1 nieznanych współczynników bk;k = 0,1,2,…,K ≤ N
Dla n-tego pomiaru (w chwili n) funkcja przyjmuje wartość
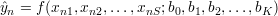 | (6) |
Charakterystyka 5 zwana jest zazwyczaj modelem matematycznym obiektu 1.
Współczynniki bk,k = 0,1,…,K wyznaczamy w taki sposób aby wyznaczone z modelu wartości ŷn jak najmniej różniły się (były jak najbliżej) od wartości zmierzonych na obiekcie yn. Najwygodniejsza jest odległość Euklidesa w przestrzeni N-wymiarowej.
![N N
Q = ∑ (y - ˆy )2 = ∑ [y - f(x ,x ,...,x ;b ,b ,b ,...,b )]2
n=1 n n n=1 n n1 n2 nS 0 1 2 K](plan6x.png) | (7) |
Funkcja ŷ = f(x1,x2,…,xs;b0,b1,b2,…,bK) gdzie współczynniki bk wyznaczone zostały tak aby minimalizować 7 nazywana bywa funkcją regresji.
Bez większej straty ogólności możemy przyjąć, że funkcje regresji są liniowe względem parametrów
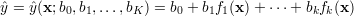 | (8) |
Przez x oznaczyłem [x1,x2,…,xS]. O funkcjach fk(x) zakłada się, że są znane i liniowo niezależne.
Popatrzmy dokładniej na proces wyznaczania współczynników bk. Załóżmy, że obiekt chcemy opisać zależnością liniową
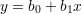 | (9) |
Dokonaliśmy N(= 9) pomiarów wartości x i y, otrzymujemy zatem N równań o postaci
 | (10) |
o dwu niewiadomych b0 i b1.
Układu (w ogólnym przypadku) rozwiązać się nie da (jest sprzeczny?) chyba, że punkty (xn,yn) leżą na prostej.2 Zatem, zamiast pierwotnego związku przyjmujemy związek zmodyfikowany:
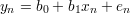 | (11) |
(i mamy teraz N równań o N + 2 niewiadomych).
Kryterium Q dane równaniem 7 dba o to, by ∑ n=1Nen2 → min!
Aby wyznaczyć b0 i b1 szukamy miejsc zerowych pochodnych cząstkowych 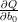 i
i
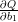
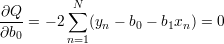 | (12) |
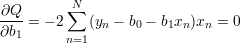 | (13) |
Otrzymany układ (liniowych) równań normalnych rozwiązujemy otrzymując:
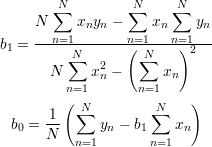 | (14) |
Co ciekawsze ∑ n=1Ne n = ∑ n=1N(y n - b0 - b1xn) = 0 Czemu?
Szukamy wielowymiarowej funkcji regresji w postaci:
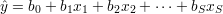 | (15) |
Obserwacje wejść i wyjść zapisane są w macierzy wejść X
 | (16) |
W macierzy tej wprowadzono elementy „fikcyjne” x10 = x20 =  = xN0 = 1
= xN0 = 1
Wyniki obserwacji wyjść obiektu oraz wyjść modelu zapiszemy jako
![′
y = [y1,y2,...,yN]](plan19x.png) | (17) |
![ˆy = [yˆ,ˆy ,...,ˆy ]′
1 2 N](plan20x.png) | (18) |
Nieznane parametry zapiszemy
![b = [b0,b1,...,bS]′](plan21x.png) | (19) |
W tym zapisie funkcja regresji przyjmuje postać
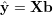 | (20) |
Kryterium
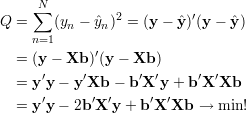 | (21) |
Podobnie jak poprzednio wyznaczamy pochodną:
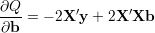 | (22) |
i otrzymujemy układ równań normalnych
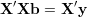 | (23) |
który rozwiązujemy
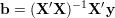 | (24) |
Łatwo sprawdzić (licząc drugą pochodną Q), że jest to istotnie minimum.
Podobne rozważania można przeprowadzić w przypadku gdy
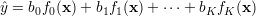 | (25) |
gdzie f0(X) = 1 jest funkcją fikcyjną.
Macierz pomiarów ma teraz postać
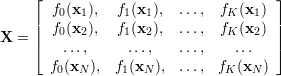 | (26) |
gdzie xn = [xn1,xn2,…,xnS]; n = 1,2,…,N.
Pozostałe rozważania są identyczne jak w poprzednim przypadku.
W praktyce funkcje f mogą przyjmować postacie
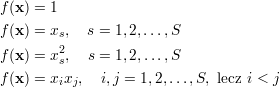 | (27) |
co daje funkcję w postaci
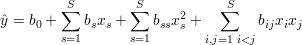 | (28) |
Aby ocenić „jakość” (natężenie związku) związku między dwiema wielkościami (wyjściem
obiektu y i wyjściem modelu 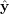 ) wyznacza się współczynnik korelacji wielowymiarowej
określony wzorem
) wyznacza się współczynnik korelacji wielowymiarowej
określony wzorem
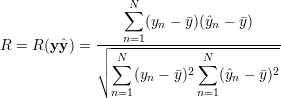 | (29) |
gdzie
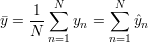 | (30) |
Do praktycznych obliczeń używa się powyższego wzoru w wersji przekształconej, macierzowej (nie wymagającej znajomości wyjść modelu ŷ).
 | (31) |
(Przekształcenie do tej postaci wymaga trochę rachunków i „zauważenia” paru rzeczy.)
Współczynnik korelacji R to liczba (0 ≤ R ≤ 1) zależna (patrz 31) od danych pomiarowych (wejść i wyjść obiektu), o których zakładaliśmy, że są zmiennymi losowymi. Zatem i R jest zmienną losową. Zatem ma jakiś rozkład. Pozwala to szacować czy wyznaczona wartość współczynnika korelacji jest bardzo prawdopodobne czy nie.
DO ZROBIENIA!
Podobnie jak wcześniej zakładać będziemy, że obiekt opisany jest równaniem
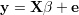 | (32) |
Przy czym teraz rozróżniamy prawdziwe wartości współczynników (β) od ich estymat (b). e to „wektor zaburzeń” normalnych o zerowej wartości średniej
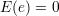 | (33) |
i niezależnych składowych, o macierzy kowariancji
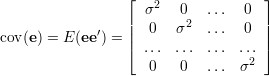 | (34) |
Wartość oczekiwana zmiennej y
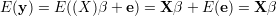 | (35) |
Kowariancja y
![{ }
cov(y) = E [y- E((y)][y - E((y)]′
= E {[X β + e - X β][X β + e- Xβ ]′} =
= E (ee ′) = Iσ2](plan39x.png) | (36) |
Ocena parametrów β wyznaczona metodą najmniejszych kwadratów to zmienna losowa
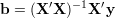 | (37) |
Wartość średnia b to
![E(b ) = E [(X ′X)-1X ′y] = (X ′X)-1X ′E(y) = (X ′X )-1X ′X β = β](plan41x.png) | (38) |
Kowariancja b
![cov(b ) = E {[b - E (b][b - E (b]′} = E [(b - β)(b - β)′]](plan42x.png) | (39) |
Wyliczmy b - β
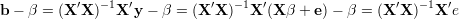 | (40) |
Zatem
![cov(b) = E {[(X ′X )-1X ′e][(X′X )-1X ′e]′} = E {(X′X )-1X ′ee′X [(X ′X )]′}](plan44x.png) | (41) |
Wzór jest dosyć symetryczny, i można go przekształcać dalej
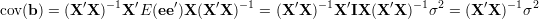 | (42) |
Macierz kowariancji mówi jakości wyznaczenia współczynników wektora b. na głównej przekątnej są wariancje składowych wektora, pozostałe wyrazy macierzy mówią jak bardzo jedna składową zależy od drugiej. Macierz jest symetryczna.
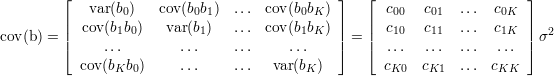 | (43) |
Współczynniki cjk zwane są mnożnikami Gaussa.
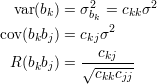 | (44) |
R(bkbj) to współczynnik korelacji między współczynnikami bk i bj.
To co jest najciekawszą cechą macierzy kowariancji cov(b) jest to, iż (w tym przypadku) zależy ona tylko od macierzy pomiarów. Oznacza to tyle, że dobierając odpowiednio wymuszenia przekazywane na obiekt możemy mieć wpływ na dokładność (i niezależność) wyznaczania parametrów funkcji regresji b.
Jeżeli uda się nam skonstruować tak macierz wymuszeń abu X′X była macierzą diagonalną, wówczas poszczególne składowe wektora b będą wyznaczane niezależnie (w sensie statystycznym) od siebie.
DOKOŃCZYĆ
Bardzo często zdarza się, że zmienne wejściowe obiektu opisanego charakterystyką
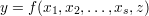 | (45) |
mają ograniczony zakres
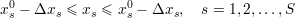 | (46) |
Dosyć naturalnym postępowaniem w takiej sytuacje jest przeprowadzenie eksperymentu polegającego na wygenerowaniu wszystkich możliwych 2S kombinacji minimalnych i maksymalnych wartości zmiennych sterujących.
Jeżeli nasz model jest liniowy
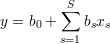 | (47) |
oraz jeżeli dokonamy zamiany zmiennych
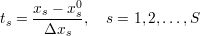 | (48) |
czyli
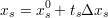 | (49) |
to nasz model ulegnie przekształceniu
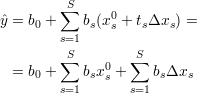 | (50) |
Powyższe możemy zapisać jako
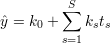 | (51) |
identyczny z pierwotnym model liniowy (o zmodyfikowanych współczynnikach).
Teraz jednak, zmienna ts przyjmuje (przy eksperymencie dwupoziomowym) wartości +1 i -1.
Gdy S = 3 macierz wejść T (przez analogie do X) przyjmie postać
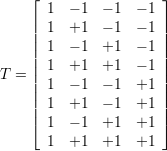 | (52) |
Wyliczmy
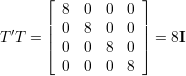 | (53) |
W przypadku ogólnym
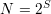 | (54) |
oraz
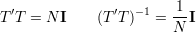 | (55) |
Natomiast współczynniki k wyliczamy z wzoru
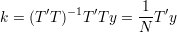 | (56) |
Gdy zmiennych wejściowych jest dużo, plan dwupoziomowy wymaga wykonania ogromnej liczby eksperymentów (gdy S = 10 wówczas 210 = 1024, gdy S = 30 trzeba wykonać 1 Gi (Giga?) pomiarów. Zakładając, że każdy eksperyment (pomiar) zajmuje tylko 1s pomiary w przypadku eksperymentu całkowitego, dwupoziomowego zajmą ponad 30 lat.
Opracowano metody wykonywania eksperymentów ułamkowych zawierających tylko pewną liczbę doświadczeń wybranych z eksperymentu całkowitego.
Jeżeli przypatrzeć się dokładniej istocie elementu całkowitego, to spełnia on trzy następujące warunki:
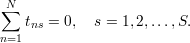 | (57) |
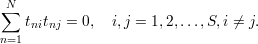 | (58) |
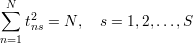 | (59) |
Najistotniejszą cechą jest ortogonalność, dzięki czemu macierz T′T jest diagonalna (co ogromnie ułatwia obliczenia i pozwala wyznaczać parametry modelu niezależnie).
Plany eksperymentów ułamkowych tworzy się tak aby spełniały warunki eksperymentu całkowitego, ale zawierały mniej punktów.
Plan całkowity eksperymentu dwupoziomowego dla trzech zmiennych (we współrzędnych
standaryzowanych:
| n | t1 | t2 | t3 |
| 1 | - | - | - |
| 2 | + | - | - |
| 3 | - | + | - |
| 4 | + | + | - |
| 5 | - | - | + |
| 6 | + | - | + |
| 7 | - | + | + |
| 8 | + | + | + |
Mając do dyspozycji 8 pomiarów można wyznaczyć co najwyżej 8 parametrów funkcji regresji (czemu?). Jeżeli nasz model ma postać:
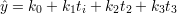 | (60) |
wszystko jest w porządku.
Pełna funkcja regresji „wielomianowej” dla trzech zmiennych będzie zawierać:
Zatem maksymalny wielomian bedzie zawierał 18 nieznanych parametrów. Żaden eksperymet dwupoziomowy nie pozwoli wyznaczyć wszystkich tych parametrów.
| n | t0 | t1 | t2 | t3 | t12 | t22 | t32 | t1t2 | t1t3 | t2t3 | t1t2t3 | t12t2 | t13 |
| 1 | + | - | - | - | + | + | + | + | + | + | - | - | - |
| 2 | + | + | - | - | + | + | + | - | - | + | + | - | + |
| 3 | + | - | + | - | + | + | + | - | + | - | + | + | - |
| 4 | + | + | + | - | + | + | + | + | - | - | - | + | + |
| 5 | + | - | - | + | + | + | + | + | - | - | + | - | - |
| 6 | + | + | - | + | + | + | + | - | + | - | - | - | + |
| 7 | + | - | + | + | + | + | + | - | - | + | - | + | - |
| 8 | + | + | + | + | + | + | + | + | + | + | + | + | + |