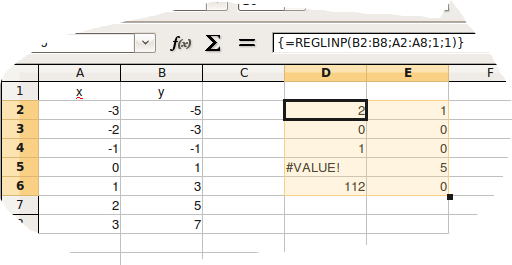
Zarówno Excel jak i program Calc z zestawu OpenOffice.org potrafią obliczać współczynniki regresji liniowej na podstawie zgromadzonych danych. Poniżej przedstawię kompletny przykład.

Dane wejściowe

Funkcja w programie Calc nazywa się REGLINP i ma cztery parametry:

1. Zakres danych gdzie zapisane są wartości Y
2. Zakres danych gdzie zapisane są wartości X
3. Gdy trzeci parametr równy jest zero, poszukujemy funkcji w postaci bez wyrazu wolnego (y = a ∗ x), gdy wartość jest różna od zera — z wyrazem wolnym (y = a ∗ x + b).
4. Czwarty parametr mówi czy mają być wyliczane tylko współczynniki (0) czy również podstawowe statystyki (1).

Jeżeli kolumna danych x zapisana jest w komórkach A2:A8, dane y w komórkach B2:B8 to wywołanie funkcji będzie miało postać:

Wyniki są następujące:

Niech teraz dane wyglądają w sposób następujący

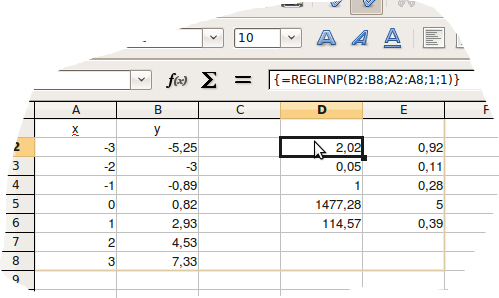
Znaczenie otrzymanych wyników jest następujące: 1. W pierwszym wierszu znajduja się wyznaczone parametry (w kolejności odwrotnej): 2,02 – oszacowanie a; 0,92 oszacowanie b 2. W drugim wierszu – błędy oszacowania parametrów 3. Trzeci wiersz oszacowanie współczynnika R² oraz błąd standardowy regresji 4. Czwarty wiersz Wartość statystyki F oraz liczba stopni swobody 5. Suma kwadratów odchyleń wartości Y obliczonych na podstawie ich średniej liniowej i suma kwadratów odchyleń wartości Y obliczonej na podstawie podanych wartości Y .

Kolejny przykład pokazuje postępowanie w przypadku funkcji z = a∗x + b∗y + c

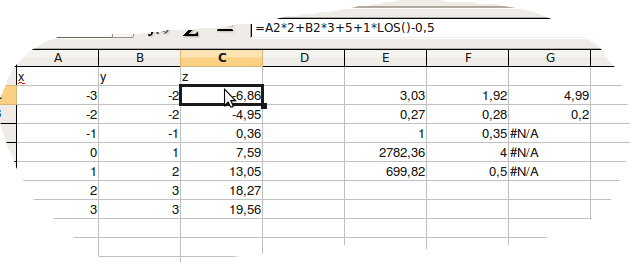
Przejdźmy teraz do naszego problemu. Szukamy aproksymacji danych w postaci:

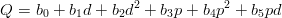(1)

Gdzie dane mają postać:

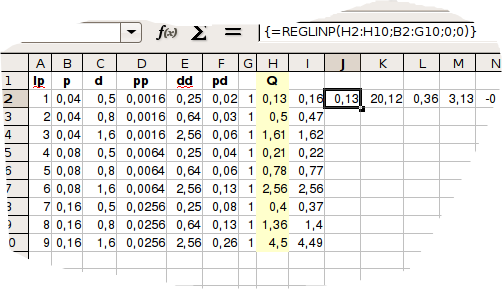
W kolumnie Q znajdują się zmierzone wartości wydatku (Q).

Wywołanie funkcji REGLINP ma postać: =REGLINP(H2:H10;B2:G10;0;0), wyliczone współczynniki wynoszą: 0,13; 20,12 ; 0,36; 3,13; -0,24; -8,91. Współczynnik podane są w kolejności odwrotnej niż kolumny macierzy X, zatem pierwsza liczba (0,13) to wyraz wolny, 20,12 to wyraz przy współczynniku p ∗ d, zatem aproksymowana funkcja ma postać:

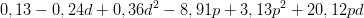(2)

Kolumna I zawiera wyliczone wartości 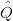czyli estymowane wartości wydatku. Jak widać przybliżenie jest całkiem dokładne.

Analiza wymiarowa problemu (z wykorzystaniem programu ADAM, podpowiada ze uwzględnienie tylko ciśnienia (p) i średnicy (d) to za mało żeby opisać proces.

Dokładniejsza analiza zjawiska podpowiada, że należy uwzględnić jeszcze lepkość cieczy η o wymiarze kg m^-1 s^-1.

Dane dla programu ADAM wyglądają następująco:
Dimensional space:
Basic units:
m (meter), kg (kilogram), s (second)
Extended units:
N (Newton - [m kg s^−2.0 ])
Quantities:
p — presure
Elements: p Dimension: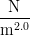
This is a scalar
d — nozzle diameter
Elements: d Dimension: m
This is a scalar
Q — expense
Elements: Q Dimension: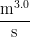
This is a scalar
eta — viscosity
Elements: eta Dimension: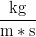
This is a scalar
Process:
Q=F(p,d,eta)

Program ADAM podpowiada, że powinniśmy poszukiwać funkcji w postaci:

(3)

Ponieważ nie możemy niezależnie wyliczyć stałej (const) i η, przyjmiemy, że funkcja ma postać:

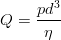(4)

i teraz na podstawie posiadanych danych musimy wyliczyć lepkość cieczy η. W tej postaci zadanie nie jest niestety liniowym problemem, który można bezpośrednio sprowadzić do regresji…

Przekształcając wzór 4 otrzymujemy:

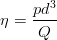(5)

I on właśnie powinien posłużyć (jak?) do wyznaczenie wartości parametru η.