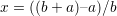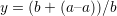Spis treści

1 Wstęp

Komputery uchodzą za mistrzów obliczeń. Dziś rozprawiamy się z tym poglądem!

1.1 Cel laboratorium

Celem laboratorium jest znalezienie przez studentów przykładów błędów popełnianych przez komputery podczas prostych obliczeń oraz oszacowanie ich wielkości.

1.2 Wymagania

1.3 Pytania

1. Konwersja liczb dziesiętnych na dwójkowe:
   • całkowitych,
   • ułamkowych.
2. Sposób zapisu liczb całkowitych (dodatnich i ujemnych) w komputerach.
3. Sposób zapisu liczb „niecałkowitych”:
   • stałoprzecinkowych,
   • zmiennoprzecinkowych.
4. Błąd bezwzględny.
5. Wartość dokładna.
6. Wartość przybliżona.

1.4 Materiały on line

• Zanurkuj w Pythonie [1]
• Dokumentacja on-line (po angielsku) [2]
• Learn Python The Hard Way (po angielsku) [4]
• Python Programming (po angielsku) [3]

2 Struktura laboratorium

3 Zadania do wykonania

1. Uruchamiamy program python
   myszka@karme:~$ python  
   Python 2.6.6 (r266:84292, Sep 15 2010, 15:52:39)  
   [GCC 4.4.5] on linux2  
   Type "help", "copyright", "credits" or "license" for more information.  
   >>>

2. Rzogrzewka
   • napisz 2*2
     >>> 2*2  
     4

   • napisz 7/2
     >>> 7/2  
     3

   • napisz 7./2
     >>> 7./2  
     3.5

   • napisz 3.1415*2
     >>> 3.1415*2  
     6.2830000000000004

3. Znajdź kolejne przykłądy (co najmniej 5 różnego typu) „źle” wykonywanych obliczeń. Dla każdego przykładu wylicz błąd bezwzględny i względny.
4. Opisz metodę konwersji liczb dziesiętnych (0.1, 3.1415, 0.3333333) całkowitych i ułamkowych na dwójkowe
   • dokonaj konwersji kilku niecałkowitych liczb dziesiętnych do postaci dwójkowej, zapisując wynik jako liczbę:
     • ośmiobitową
     • szesnastobitową
     • trzydziestodwubitową
   • w każdym przypadku dokonaj konwersji odwrotnej i policz błąd bezwzględny i względny
5. Sprawdź, dla jakich różnic wykładników komputer zacznie (będzie) prawidłowo wyliczać wartość wyrażenia x. Dla przypomnienia: demonstrowany na wykładzie przykład to a = 1.0e+20 oraz b = 1.0e-20
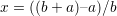
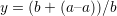
6. Najpierw zastanów się jaka „powinna” być wartość x i y!

4 Materiały pomocnicze

4.1 Python

Python jest językiem programowania wysokiego rzędu przeznaczonym do rozwiązywania najróżniejszych zadań (język programowania ogólnego przeznaczenia). Historia jego jest już dosyć długa: używany jest od 19 lat.

Może być stosowany do tworzenia różnego rodzaju aplikacji, ale także do prowadzenia obliczeń w trybie doraźnym (ad-hoc).

Python jest wykorzystywany bardzo szeroko: standardowo dołączany jest do systemu Linux i Mac OS. Używany jest bardzo szeroko przez:

• Google,
• YouTube,
• BitTorrent został napisany w Pythonie,
• Industrial Light & Magic, Pixar, używają oprogramowania napisanego w Pythonie do produkcji swoich filmów animowanych,
• …

Dla osób znających inne języki programowania pomocne mogą być zestawienia umieszczone w serwisie Hyperpolyglot Programming Languages Reference Sheets.

4.2 Uruchomienie

Obliczenia „ad-hoc”:

1. Programy → Programowanie → Python
2. Programy → Akcesoria → Terminal; w otwartym okienku piszemy python

Przygotowanie i uruchomienie programu:

1. Korzystając z dowolnego edytora tekstowego (polecam gedit) tworzymy plik o rozszerzeniu .py (na przykład test.py) i wpisujemy do niego program.
2. Otwieramy terminal (Programy → Akcesoria → Terminal) i w tym terminalu piszemy python test.py

Utworzenie samodzielnej aplikacji:

1. Tworzymy plik z programem (test.py) za pomocą dowolnego edytora pamiętając aby jako pierwsza linia wystąpiło:
   #!/usr/bin/env python

2. Po zapisaniu pliku nadajemy mu „atrybut wykonywalności” pisząc w terminalu
   chmod +x test.py

   albo odpowiednio modyfikujemy właściwości pliku (prawy klawisz myszy na pliku w menedżerze plików i wybieramy Właściwości i w zakładce Uprawnienia ustawiamy ptaszka przy „Zezwolenie na wykonywanie pliku jako programu”.

3. Aplikację uruchamiamy poleceniem
   ./test.py

   w terminalu lub klikając myszą w menedżerze plików.

4.3 Operacje arytmetyczne

Podstawowe operacje (+,−,∗) działają tak jak można się spodziewać. Operacja dzielenia (∕) może sprawiać pewne kłopoty:

Dopiero napisanie

daje oczekiwany efekt.

Potęgowanie oznaczane jest znakiem ∗∗, zatem 3 do potęgi trzeciej (3³) wygląda tak:

Inne operatory arytmetyczne to % — reszta z dzielenia albo modulo: 3 dzielone przez dwa to 1 (bo dwójka mieści się w trójce całkowicie jeden raz) i reszta 1:

W bardziej skomplikowanych obliczeniach można posługiwać się podstawowym zestawem funkcji (tak zwane funkcje wbudowane):

• abs wartość bezwzględna
• divmod(a,b) zwraca wynik dzielenia całkowitoliczbowego i resztę z dzielenia jako parę liczb
  >>> 3./2  
  1.5  
  >>> 2/2.  
  1.0  
  >>> 3/2.  
  1.5  
  >>>

• float konwertuje liczbę do postaci zmiennoprzecinkowej
  >>> float(3)  
  3.0

• round(x[,n]) zaokrągla liczbę do n miejsc po przecinku:
  >>> round(3.1415)  
  3.0  
  >>> round(3.1415,3)  
  3.1419999999999999  
  >>> round(3.1415,2)  
  3.1400000000000001  
  >>> round(3.1415,1)  
  3.1000000000000001

Użycie innych funkcji matematycznych wymaga specjalnych zabiegów: podpowiedzenia programowi, że będziemy chcieli z nich korzystać:

mówi, że zechcemy używać modułu math zawierającego różne funkcje i stałe matematyczne. Po wydaniu tego polecenia możemy napisać:

Dostępne stają się funkcje trygonometryczne, hiperboliczne, logarytmiczne i wykładnicze, funkcje specjalne oraz stałe: π i e

4.4 Obliczenia

W prostych obliczeniach można korzystać z pythona jak z podręcznego kalkulator: wyniki obliczeń podawane będą na bieżąco. Można też wyniki zapamiętywać (coś jak pamięci kalkulatora). Z tym, że poszczególne pamięci możemy nazywać według naszego uznania:

Podanie w linii nazwy pamięci (zmiennej) powoduje wydrukowanie jej wartości:

4.5 Bloki instrukcji

Cechą odróżniającą język python od innych języków (Na przykład C czy Pascal) jest sposób wyróżniania bloków instrukcji. W języku C używa się do tego nawiasów klamrowych {}, a w języku Pascal słów kluczowych begin i end.

W pythonie używa się „wcięć”.

Potrzeba korzystania z bloków instrukcji pojawia się, między innymi:

1. podczas wykonywania instrukcji warunkowych,
2. przy tworzeniu pętli,
3. podczas definiowania funkcji.

Na przykład:

Poniżej przykład programu rozwiązującego równanie kwadratowe:

Uwagi:

1. Program można sobie ściągnąć i zapisać: trojmian.py, a później uruchomić w terminalu wypisując python trojmian.py.
2. Funkcji float została użyta aby skonwertować tekst (ciąg znaków) do liczby. Informacje wczytywane z terminala funkcją raw_input są typu tekstowego!

4.6 Instrukcje warunkowe

Instrukcja warunkowa używana jest podczas programowania do wprowadzenia rozgałęzienia w zależności od wartości jakiegoś parametru czy spełnienia jakiegoś warunku. Typowy przykład konieczności wprowadzenia instrukcji warunkowej to program wyliczania rzeczywistych miejsc zerowych trójmianu kwadratowego. W zależności od wartości parametru Δ albo wyliczamy jeden pierwiastek rzeczywisty, albo dwa, albo musimy stwierdzic, że pierwiastków rzeczywistych nie ma.

Fragment programu wyliczającego pierwiastki przedstawiono w poprzednim rozdziale. (Tam gdzie się kończy wcięcie — kończy się zakres działania odpowiedniego fragmentu warunku.)

4.7 Pętle

Pętla to taka konstrukcja programistyczna, która nakazuje wykonanie jakiejś czynności:

• kilka razy
  for i in range(3,12) : 
          print i
• tak długo aż jakiś warunek zostanie spełniony.
  i=3 
  while i < 12 : 
          print i 
          i = i+1

W obu powyższych przypadkach efekt powinien być taki:

(Oczywiście nie ma wielkiej różnicy pomiędzy tymi sytuacjami, ale, tradycyjnie, robione jest takie rozróżnienie).

5 Wersja PDF instrukcji

Wersja PDF instrukcji.

Literatura