Spis treści

1 Wstęp

Tak nieszczęśliwie się złożyło, że niektóre grupy będą miały siedem laboratoriów inne zaś osiem (co zależy od parzystości tygodnia).

Zatem ostatnie laboratorium (ostatnie dwa laboratoria) poświęcone będą programowaniu w języku Python.

Tematyka zajęć w kolejnym semestrze będzie obejmowała programowanie w języku C — nie powinien to być specjalny problem.

Studenci na zajęciach siódmych rozpoczynają realizację zadań od „wprawek” (rozdział 2), a następnie kontynuują zadania do wykonania (rozdział 3) tyle ile dadzą rady. Im kto więcej zrobi tym lepsza ocena.

Zatem dla tych, którzy istotnie mają zajęcia ósme:

• powinny być one potraktowane w pierwszej kolejności jako zajęcia „odróbkowe”
• można też kontynuować zadania z laboratorium siódmego.

1.1 Cel laboratorium

Celem laboratorium jest zmierzenie się z (nowym?) językiem programowania i zaprogramowanie bardzo prostych problemów. Przy czym chciałbym aby samo programowanie poprzedzone było narysowaniem prostego schematu blokowego. Jako podstawowy zestaw bloków stosowanych na schematach blokowych można przyjąć ten z Wikipedii.

1.2 Wymagania

Zapoznanie się z elementarną dokumentacją programu Python (instrukcja laboratoryjna nr 4 [1] i/lub bardziej zaawansowaną dokumentacją po polsku dostępną on-line [2].

1.3 Materiały

1.3.1 Funkcje

Bardzo często programując w jakimś języku programowania musimy skorzystać z jakiejś funkcji. Python dostarcza bardzo wiele funkcj, a na przykłąd najbardzie podstawowe funkcje matematyczne dostępne są w module math. Na początkuy programu piszemy:

a poźniej możemy z funkcji korzystać swobodnie:

(Sprawdź jaki będzie wynik!)

Mozemy również zdefiniować własną funkcję. Będzie to funkcja f(x) = 3x² − 5x + 2. (Zwracam uwagę na wcięcie!)

Po jej zdefiniowaniu możemy już funkcji używać:

albo

albo

W powyższym przykładzie x jest zmienną niezależną (tak jak w funkcji sin(x)), a polecenie return powoduje wyliczenie wartości i „podstawienie jej pod f(x)”. Funkcję można zdefiniować również tak:

Teraz polecenie return zwraca (wyliczoną wcześniej) wartość y jako wartość funkcji f(x).

1.3.2 Rekurencja

Poniżej rekurencyjna definicja funkcji silnia

Sprawdź czy funkcja działa.

2 Struktura laboratorium

Zaczynamy od wprawek.

1. Co robi ta instrukcja? Jaki będzie wyniki? Sprawdź! Zobacz co się będzie działo gdy zmienisz wartość a (na ujemną, na przykład). (Poniżej ␣ oznacza odstęp.)
   a = 5 
   if a > 0: 
       print ”a_dodatnie!” 
   else: 
       print ”a_ujemne!”

   Zmodyfikuj program tak, by rozpoznawał przypadek gdy a jest równe zero i informował o tym.

2. Co robi ten program? Jaki będzie wynik?
   for i in range(7, 9) 
       print i

   Zmodyfikuj go tak aby drukował tablicę funkcji x² dla x zmieniającego się od -10 do 10 włącznie.

3. Co robi poniższy program?
   a = 1536 
   while a%2 == 0: 
       a = a/2 
       print a

   Przy okazji, jaki będzie wynik programu?

   while 1: 
      print ”Dosc!”

   A tego:

   while 0: 
      print ”Dosc!”

   Peksperymentuj i opisz działanie instrukcji while.

3 Zadania do wykonania

3.1 Rekurencyje wyliczanie wartości Największego Wspólnego Dzielnika

Wariant rekurencyjny wyznaczania NWD wygląda jakoś tak: gcd(k,n) = n gdy k = 0 natomiast gcd(k,n) = gcd(n mod k,k) gdy k > 0.

Zadania

1. Zaprogramuj w Pythonie funkcję gcd.
2. Porównaj wyniki liczone każdą z trzech metod.

3.2 Ciąg Fibonacciego

Ciąg Fibonacciego jestjednym z wielu przykładów „operacji” zdefiniowanej rekurencyjnie.

Zadaniem jest zaprogramowanie (w Pythonie) rekurencyjnej funkcji wyliczającej zadany wyraz ciągu.

Dodatkowo programpowinien zliczać liczbę wywołań funkcji. W tym celu należy jedną zmienna przeznaczyć na licznik i zaraz po wejściu do funkcji zwiększać ten licznik o jeden.

Przed zakończeniem obliczeń program powinien wyswietlać wyliczony wyraz ciągu oraz liczbę wywołań funkcji.

3.3 Algorytm E

Oto jedna z jego wersji algorytmu Euklidesa: Dane są dwie dodatnie liczby całkowite m i n, należy znaleźć ich największy wspólny dzielnik (NWD) tj. największą dodatnią liczbę całkowitą, która dzieli całkowicie zarówno m jak i n.

1. [Znajdowanie reszty] Podziel m przez n i niech r oznacza resztę z tego dzielenia. (Mamy 0 ≤ r < n.)
2. [Czy wyszło zero?] Jeśli r = 0 zakończ algorytm; odpowiedzią jest n.
3. [Upraszczanie] Wykonaj m ← n, n ← r i wróć do kroku 1.

Schemat blokowy

Zadania

1. Spróbuj zaprogramować w Pythonie Algorytm E.

3.4 Algorytm B

1. Przyjmij k ← 0, a następnie powtarzaj operacje: k ← k + 1, u ← u∕2, v ← v∕2 zero lub więcej razy do chwili gdy przynajmniej jedna z liczb u i v przestanie być parzysta.
2. Jeśli u jest nieparzyste to przyjmij t ←−v i przejdź do kroku 4. W przeciwnym razie przyjmij t ← u.
3. (W tym miejscu t jest parzyste i różne od zera). Przyjmij t ← t∕2.
4. Jeśli t jest parzyste to przejdź do 3.
5. Jeśli t > 0, to przyjmij u ← t, w przeciwnym razie przyjmij v ←−t.
6. Przyjmij t ← u−v. Jeśli t ⁄= 0 to wróć do kroku 3. W przeciwnym razie algorytm zatrzymuje się z wynikiem u ⋅ 2^k.

Zadania

1. Narysuj schemat blokowy algorytmu B
2. Spróbuj zaprogramować w Pythonie Algorytm B.

3.5 Metoda Newtona-Raphsona: pierwiastek dowolnego stopnia

Załóżmy, że mamy wyznaczyć pierwiastek stopnia n z liczby w, czyli znaleźć taką liczbę x, że:

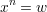(1)

lub inaczej:

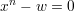(2)

Jeżeli oznaczymy f(x) = xⁿ −w to zadanie to można zapisać ogólniej: należy znaleźć takie x, że f(x) = 0.

Jeżeli zadanie dodatkowo uprościmy zakładając:

• funkcja ma dokładnie jedno miejsce zerowe,
• jest różniczkowalna,
• jej pochodna w całym przedziale jest albo dodatnia albo ujemna;

to możemy naszkicować następujący rysunek ilustrujący nasze zadanie: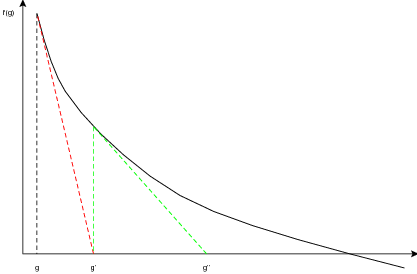

Zaczynamy w punkcie g; wartość funkcji w tym punkcie wynosi f(g). Musimy w jakiś sposób zdecydować w którym kierunku należy wykonać następny krok. Zauważmy, że możemy w tym celu wykorzystać pochodną (czerwona, przerywana linia na powyższym rysunku). Jeżeli przybliżymy funkcję za pomocą pochodnej (stycznej do funkcji, przechodzącej przez punk (g,f(g) to następnym przybliżeniem będzie punkt przecięcia stycznej z osią x.

Z równania prostej mamy:

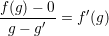(3)

czyli

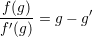(4)

i dalej

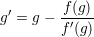(5)

Jeżeli zauważymy, że f(x) = xⁿ − w oraz, że f′(x) = nxⁿ⁻¹ to kolejne przybliżenie wyliczane będzie ze wzoru:

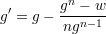(6)

albo

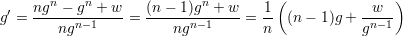(7)

Gdy n = 2, wówczas

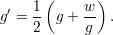(8)

3.5.1 Realizacja programowa

Program będzie się składał z trzech części:

1. blisko(a, b) – funkcja o wartościach logicznych sprawdzająca czy |a − b|≤ ε,
2. lepszy(w, g) – funkcja rzeczywista wyliczająca następne, lepsze przybliżenie pierwiastka,
3. pierwiastek(n, w, g) – funkcja (rzeczywista) wyliczająca pierwiastek stopnia n z w zaczynając od przybliżenia g.

3.5.2 Zadania treningowe

1. Narysować schematy blokowe poszczególncyh funkcji.
2. Zaprogramować w języku Python program wyliczający dla zadanej liczby, z wykorzystaniem trzech powyższych funkcji, pierwiastek z zadanej (wczytanej) (bez rekurencji!).
3. Zaprogramować wersję „rekurencyjną” powyższego algorytmu.

4 Materiały pomocnicze

4.1 Potrzebne instrukcje języka Python

1. Instrukcja warunkowa
2. Instrukcja while
3. Definicje funkcji

5 Wersja PDF dokumentu

Wersja PDF dokumentu

Literatura