Created wtorek 13 październik 2009
1. Model liniowy. Jest to sytuacja najprostsza. Mamy pary punktów
\{x_i, y_i\}, i=1,2,\ldots N
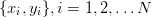
x_i to zmienne niezależne, y_i zmienne zależne. Szukamy zależności łączącej te wielkości. Jeżeli możemy przyjąć, że
y=ax+b
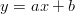
To mówimy o regresji liniowej. Szczególnym przypadkiem jest sytuacja gdy b=0 czyli y=ax (Jest to przypadek bardzo ważny z fizykalnego punktu wiedzenia -- całkiem często zdarza się, że ze nasze zjawisko ma tę właściwość, że w przypadku gdy zmienna niezależna (wejście)równa się zero to również wyjście (zmienna zależna) powinna mieć wartość zero. W sytuacjach praktycznych, gdy urządzenie pomiarowe wprowadza błąd systematyczny -- może być trudno...
Aby wyznaczyć parametry a i b możemy posłużyć się metodą ,,interpolacji lub ,,aproksymacji.
Gdy N=2, a i b wyznaczamy rozwiązując układ równań
y_1 = a x_1 + b
y_2 = a x_2 + b
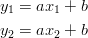
(wyznaczamy parametry prostej przechodzącej przez dwa punkty).
Gdy b musi być równe 0, wówczas potrzebujemy tylko jednego pomiaru i wyznaczamy a=y_1/x_1.
Gdy pomiarów jest więcej niż parametrów do wyznaczenia musimy zdecydować się na jakiś kompromis: wybrać a i b w taki sposób aby ,,było dobrze. Ponieważ rzadki kiedy ,,dobrze nas zadowala staramy się postępować najlepiej, czyli parametry a i b wyznaczać w wyniku rozwiązania zadania optymalizacji
Q=f(a, b, x_i, y_i, i=1,2,\ldots,N) -> min!
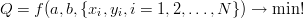
Czyli mamy wybrać parametry a i b tak, żeby dla danego zestawu danych pomiarowych uzyskać najmniejszą wartość funkcji (funkcjonału) Q. Funkcjonał/funkcję Q zazwyczaj konstruuje się tak, żeby jej wartość w jakiś sposób odzwierciedlała błąd tyczenia prostej y=a x + b. Na przykład tak:
Q=\sum_{i=1}^N |a x_i +b -y_i|
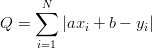
czyli chcemy tak wyznaczyć a i b aby sumaryczne ,,odległości'' między tyczoną prostą a punktami były najmniejsze. Odległość wyznaczana jest jako |a x_i +b -y_i|.
Zdajemy sobie sprawę, że wartość bezwzględna nie ułatwia obliczeń tylko je utrudnia, więc zastąpimy ją funkcją kwadratową:
Q=\sum_{i=1}^N (a x_i +b -y_i)^2
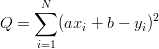
Z nią to już wiadomo co robić.
a) liczymy pochodne i przyrównujemy do zera
dQ/da = 0
dQ/db = 0
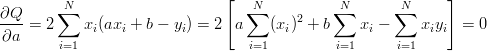
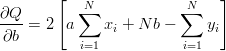
b) rozwiązujemy powyższy układ równań (jeżeli nie ma tam błędu, jak jest -- rozwiązujemy właściwy)
Uwagi.
Szkic rozwiązania: podstawiając
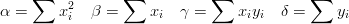
Dostajemy układ równań (zwany układem równań normalnych)
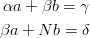
(i tu możemy wykorzystać Matlaba, Mathematicę albo cokolwiek innego, żeby układ rozwiązać).
Rozpatrzmy teraz przypadek gdy x jest wektorem wymuszeń, a y skalarem. Funkcję, której parametry chcemy identyfikować zapisujemy tak:
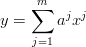
gdzie j to numer składowej, a -- wektor nieznanych parametrów, x --wektor wymuszeń. Dalej idąc w wektory możemy to zapisać jako iloczyn skalarny
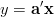
(gdzie ' to symbol transpozycji).
Kryterium Q zapisuje się w formie klasycznej jako
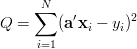
(dolny index to numerek pomiaru).
Jeżeli jednak utworzymy macierz X której kolejnymi kolumnami są wektory x_i
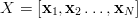
utworzymy wektor (kolumnowy) Y, którego kolejnymi składowymi są y_i:
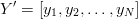
to teraz mamy:
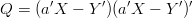
Powyższe nazywa się formą kwadratową i może być przekształcone do postaci:
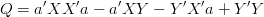
W powyższym równaniu każdy ze składników jest liczbą (bo i Q jest liczbą) zatem dwa środkowe wyrazy są sobie równe (czemu?).
Szukanie minimum formy kwadratowej jest tak samo łatwe/trudne jak i w poprzednim przypadku. Zwracam uwagę, że teraz pochodna Q po całym wektorze parametrów będzie macierzą co w pierwszej chwili może wystraszyć... Przyrównywanie pochodnych do zera prowadzi do rozwiązywania układów równań (ale na szczęście liniowych). Niezbyt skomplikowane przekształcenia pozwalają wyznaczyć a jako
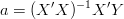
Powyższe jest możliwe do realizacji gdy X'X jest macierzą nieosobliwą (co to znaczy!?)
Nasz zapis (a'x) nie uwzględnia wyrazu wolnego. Jeżeli formalnie zmodyfikujemy zapisy dodając do zmiennych niezależnych składową stale równą 1
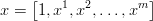
to problem ten rozwiążemy.
W świecie realnym mamy do czynienia z wartościami, które... nie są do końca znane, przewidywalne,...
Czasami sobie życie upraszczamy mówiąc że te wartości to zmienne losowe, a my jedynie "oglądamy" ich realizacje. Zadanie regresji opisywane jest wówczas jakoś tak:
1 Mamy zmienną losową y, która ma rozkład (normalny) z wariancją σ^2 i ze średnią
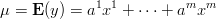
zależną oz zmiennych x^j i stałych parametrów a^j
2 To co obserwujemy (y_i) to μ_i zaburzone jakimś e_i
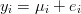
3 Ponieważ e = y - μ to kryterium Q oznacza minimalizowanie e'e
Wszystkie rozważania statystyczne prowadzi się najlepiej gdy rozkłady są normalne, o wszystkim co się da możemy powiedzieć że jest niezależne, nieskorelowane i generalnie jest OK
Mamy teraz model, który, bardzo ogólnie) jest nieliniową funkcją zmiennej wejściowej i parametrów:
y=F(x, a)
parametry a można wyznaczyć w postępowaniu podobnym jak wyżej starając się je dobrać tak, by
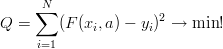
Jeżeli uda się nam znaleźć miejsca zerowe pochodnej Q po a to bardzo dobrze, jeżeli nie -- pozostają metody numeryczne szukania minimum funkcji.
Bardzo często do opisu zjawiska używamy wielomianów czyli funkcji o postaci
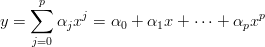
(z wymiarowego punktu widzenia, gdy zmienna fizyczna ma jakąś interpretację, wówczas, aby powyższy zapis miał sens poszczególne współczynniki α muszą mieć też wymiar; pytanie jaki wtedy będzie ich sens fizyczny? Może lepiej zastosować metody analizy wymiarowej i sprowadzić model do funkcji liczbowo-liczbowej? O tym będzie mowa kiedy indziej.)
RegresjaII Czyli więcej statystyki