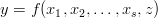
Created wtorek 27 październik 2009
Mamy obiekt opisany równaniem
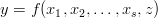
W praktyce nie mamy jednak do czynienia z zależnościa fumkcyjną, a jedynie zależnością stochastyczną: dla tego samego zestawu danych wejściowych możemy uzyskać zupełnie inne wyniki!)
O zależności stochastycznej zmiennej losowej Y od zmiennej losowej X mówimy gdy mamy do czynienia jednoznaczną zależnością rozkładu prawdopodobieństwa Y od wartości x przybranej przez zmienną X.
Podczas budowy modelu matematycznego zjawiska interesowaćnaz będzie wartość oczekiwana zmiennej losowej Y przy warunku X=x. Jeżeli
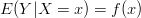
to mówimy o korelacji pomiędzy Y i X.
Załóżmy, że w N chwilach znane są wartości wejść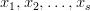 
oraz odpowiadająca im wartość wyjścia obiektu y. Dane te grupujemy w tablicy obserwacji wejść i wyjść
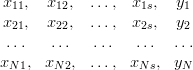
Naszym zadaniem jest wyznaczenie charakterystyki "zastępczej" (ale nie zawsze!) zależnej od K+1 nieznanych współczynników
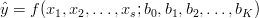
Współczynniki b wyznaczamy minimalizując (maksymalizując) pewien wskaźnik jakości przybliżenia: zazwyczaj kwadrat różnicy.
Gdy funkcja regresji ma postać:
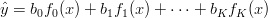
Macierz wejść uogólnionych ma postać
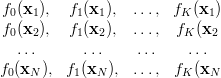
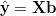
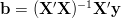
Do określenia natężenia związku między y a x używa się współczynnika korelacji
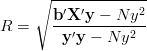
(y powinno mieć kreskę -- że średnia)
Istotność współczynnika korelacji badamy za pomocą testu F Snedecora (wpisać!)
Gdy
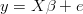
oraz
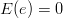
i macierz kowariancji
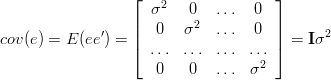
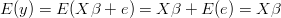
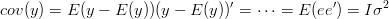
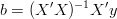
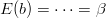
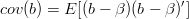
ponieważ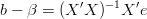 
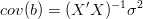
Macierz ta mówi jak bardzo wyznaczone parametry b są od siebie zależne.
Jeżeli zacząć teraz testować wartości współczynników b (test F Snedecora) uzyskamy pewien obszar ufności (elipsoida K+1 wymiarowa)
...
(
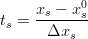
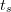nie przekraczają jedynki)
Eksperyment wykonuje się tak, że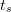 
przyjmują wartości skrajne... +1 i -1
W przypadku przeprowadzenia eksperymentu pełnego (t przyjmują wszystkie możliwe warianty wartości skrajnych) T'T jest macierzą o zerowych elementach poza główną przekątną: parametry wyznaczone w sposób niezależny i łatwo się oblicza...
(Mańczak Technika planowania eksperymentu, 1976 sygnatura 276180L/1)